Em matemática e ciência da computação, uma definição recursiva, ou definição indutiva, é usada para definir os elementos em um conjunto em termos de outros elementos no conjunto

Alguns exemplos de objetos definíveis recursivamente incluem fatoriais, números naturais, números de Fibonacci, as pastas e subpastas em sistemas de arquivos, etc.


def factorial(n):
    if n < 2:
        return 1
    else:
        return n * factorial(n-1)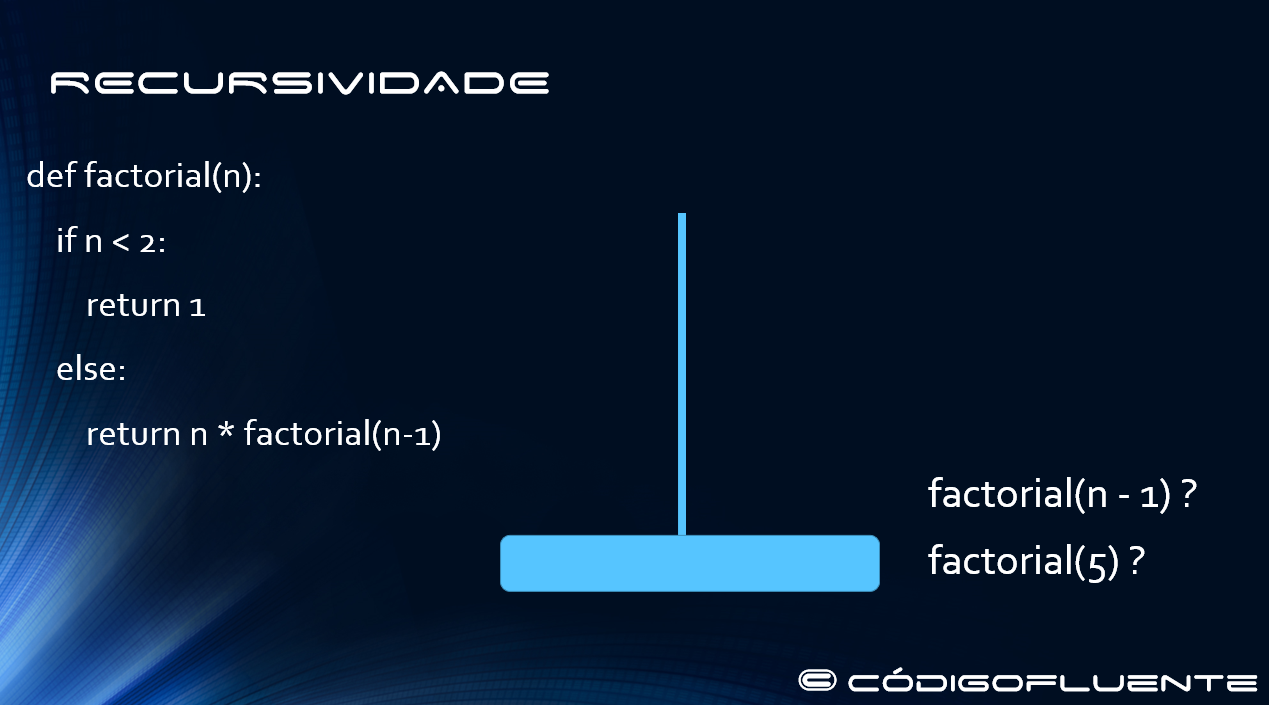

Recursividade fatorial de 5 figura inicial

Recursividade fatorial de 5 figura final

A solução iterativa é mais eficiente.


def factorial(n):
    fact = 1
    for num in range(2, n + 1):
        fact *= num
    return fact

Aula 06 – Subsequência Comum Mais Longa – LCS ( longest common subsequence )

LCS é o problema de encontrar o tamanho da subsequência mais longa comum a todas as sequências em um conjunto de sequências (geralmente apenas duas sequências).

É diferente do problema da mais longa substring comum, em que as subsequências precisam ocupar posições consecutivas nas sequências originais.

  ABABC
    |||
   BABCA
    |||
    ABCBA

O problema da subsequência comum mais longa(LCS) é um problema clássico de ciência da computação, a base de programas de comparação de dados como o utilitário diff, e tem aplicações em linguística computacional e bioinformática.

Ele também é amplamente usado por sistemas de controle de revisão, como o Git, para reconciliar várias alterações feitas em uma coleção de arquivos controlada por revisão.

Longest Common Subsequence (LCS)

Dadas duas sequências, encontre o comprimento da maior subsequência presente em ambas.

Uma subsequência é uma sequência que aparece na mesma ordem relativa, mas não necessariamente contígua.

String X	F	C	A	B
String Y	A	B	D	C

Teríamos a saída: 2 (A, B) o C não porque tá fora da ordem.

Se a gente for gerar todas as subsequências possíveis, teríamos uma árvore mais ou menos assim:

Veja que temos algumas computações repetidas, parecido com o que foi mostrado na aula-04-fibonacci-com-programacao-dinamica.

Essa abordagem do problema não é eficiente em termos de complexidade, porque sua complexidade é de O(2^N), no caso de duas sequências, isso quer dizer que temos uma complexidade exponencial.

Se a gente tem uma sequência de tamanho N e gastou X tempo pra fazer isso, se formos comparar duas sequências de tamanho N + 1, vamos gastar 2^X+1 tempos para comparar.

Então no caso de duas sequências:

ABC e CBD leva 2^3 = 8 tempos

ABCD e BDCF leva 2^4 = 16 tempos

ABCDGHJ e BDCFIKL leva 2^7 = 128 tempos

A medida que o N cresce, a complexidade aumenta exponencialmente.

Veja essa implementação ingênua:


#!/bin/python3
import time
# Function to find the length of the longest common subsequence of
# sequences `X[0…m-1]` and `Y[0…n-1]`
def lcs(X, Y, m, n):
    #m = 6
    #n = 5
 
    # return if the end of either sequence is reached
    if m == 0 or n == 0:
        return 0
 
    # if the last character of `X` and `Y` matches
    if X[m - 1] == Y[n - 1]:
        return lcs(X, Y, m - 1, n - 1) + 1
 
    # otherwise, if the last character of `X` and `Y` don't match
    return max(lcs(X, Y, m, n - 1), lcs (X, Y, m - 1, n))

#m = 5
#n = 6
#Range: i => 0 to 6
#Range: j => 0 to 7
#end of function lcs 

#X = [1, 2, 3, 4, 1]
#Y = [3, 4, 1, 2, 1, 3]

#L matrix final
#   j = columns
#i  0  1  2  3  4  5  6
#0 [0, 0, 0, 0, 0, 0, 0], 
#1 [0, 0, 0, 1, 1, 1, 1], 
#2 [0, 0, 0, 1, 2, 2, 2], 
#3 [0, 1, 1, 1, 2, 2, 3], 
#4 [0, 1, 2, 2, 2, 2, 3], 
#5 [0, 1, 2, 3, 3, 3, 3]

if __name__ == '__main__':

    m, n = input().split()
    n = int(n)
    m = int(m)
    a = list(map(int, input().rstrip().split()))
    b = list(map(int, input().rstrip().split()))
    
    print('m: ' + str(m))
    print('n: ' + str(n))
    print(a)
    print(b)

    t0= time.process_time() 
    print('O tamanho da maior subsequência comum é: ' + str(lcs(a, b, m, n)))
    t1 = time.process_time() - t0 
    print("Tempo gasto: ",abs(t1 - t0))

Usando programação dinâmica

Vamos usar programação dinâmica para reduzir a complexidade para O(n^2), uma complexidade quadrática.

Usando programação dinâmica, a gente vai evitar computações repetidas, desnecessárias, porque já foi feita antes.

A programação dinâmica armazena as computações já feitas e quando se depara com o calculo de algo que já fez antes, que já tem o resultado, ele não vai precisar recalcular, apenas pegar o resultado já calculado para aquela entrada, e retornar.

Implementação com programação dinâmica:


#!/bin/python3
import time
# Mais longa subsequência comum.
def lcs(X , Y, m, n):
    # length of the strings 
    #m = 5
    #n = 6
    # array para armazenar as computações(valores de programação dinâmica) 
    L = [[None] * (n + 1) for i in range(m + 1)] 
  
    """Seguindo as etapas para construir o L[m + 1][n + 1] ascendentemente 
    Nota: L[i][j] contém o tamanho de LCS de X[0..i - 1] 
    and Y[0..j - 1]"""
    for i in range(m + 1): 
        for j in range(n + 1): 
            #caso base
            if i == 0 or j == 0 : 
                L[i][j] = 0
            #
            elif X[i - 1] == Y[j - 1]:
                L[i][j] = L[i - 1][j - 1] + 1
            else: 
                L[i][j] = max(L[i - 1][j] , L[i][j - 1])
  
    # L[m][n] contém o tamanho de LCS de X[0..n-1] & Y[0..m-1] 
    return L[m][n]

if __name__ == '__main__':
    m, n = input().split()
    n = int(n)
    m = int(m)

    a = list(map(int, input().rstrip().split()))
    b = list(map(int, input().rstrip().split()))

    print('m: ' + str(m))
    print('n: ' + str(n))
    print(a)
    print(b)
    
    t0= time.process_time()
    print('O tamanho da maior subsequência comum é: ' + str(lcs(a, b, m, n)))
    t1 = time.process_time() - t0
    print("Tempo gasto: ",abs(t1 - t0))