Aula 05 – Complexidade de Fibonacci O(n) iterativa e O(1) pela fórmula
Aula 05 – Complexidade de Fibonacci O(n) iterativa e O(1)

Fibonacci O(n) iterativa e O(1) pela fórmula
Voltar para página principal do blog
Todas as aulas desse curso
Aula 04 Aula 06
Se gostarem do conteúdo dêem um joinha 👍 na página do Código Fluente no
Facebook
Esse é o link do código fluente no Pinterest
Meus links de afiliados:
Hostinger
Digital Ocean
One.com
Meu github:
https://github.com/toticavalcanti
Implementações de Fibonacci O(n) iterativa e O(1) pela fórmula
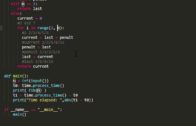
O(n) iterativa
# Programa para encontrar o enésimo número de fibonacci em Python 3
# com complexidade O(n), implementação iterativa.
import time
def fib(n):
last = 1
penult = 1
if n == 1:
return penult
elif n == 2:
return last
else:
current = 0
for i in range(2, n):
current = last + penult
penult = last
last = current
return current
def main():
n = int(input())
t0= time.process_time()
print( fib(n) )
t1 = time.process_time() - t0
print("Time elapsed: ",abs(t1 - t0))
if __name__ == "__main__":
main()
Veja que temos um for i in range(2, n), já que os casos bases 0 e 1, ou seja, o primeiro e segundo número da sequência é 1, por isso não precisa ser calculado.
Na verdade é um for de tamanho n – 2, mas isso não faz diferença, como a complexidade tá relacionada ao tamanho do n, é uma complexidade de O(n).
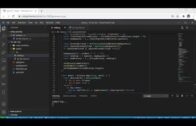
Implementação mágica, O(1).
Agora a implementação mágica, a complexidade é de O(1), isto é, constante, porque simplesmente é só uma conta que tem que ser feita, só um cálculo, não precisa fazer nenhum loop.
A complexidade nesse caso não depende do tamanho do n.
A implementação segue essa fórmula:
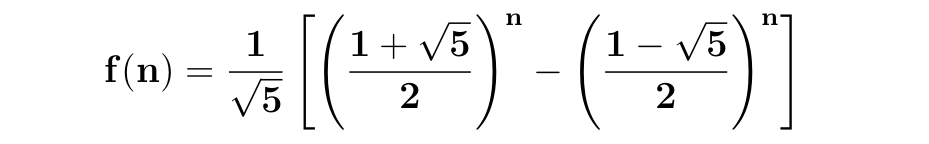
Fórmula de fibonacci
O(1) Fórmula
# Programa para encontrar o enésimo número de fibonacci em Python 3
# com complexidade O(1)
import time
import math
def fib(n):
# phi é o número de ouro, número áureo, secção áurea,
#proporção de ouro, é uma constante real algébrica irracional
#Seu valor é 1.618033988749895... ao infinito
phi = (1 + math.sqrt(5)) / 2
return round(math.pow(phi, n) / math.sqrt(5))
def main():
n = int(input())
t0= time.process_time()
print( fib(n) )
t1 = time.process_time() - t0
print("Time elapsed: ",abs(t1 - t0))
if __name__ == "__main__":
main()