Aula 16 – Scikit-Learn – Reconhecimento facial – Treinamento do modelo SVM
Aula 16 – Scikit-Learn – Reconhecimento facial – Treinamento do modelo SVM
Voltar para página principal do blog
Todas as aulas desse curso
Aula 15 Aula 17
Script dessa aula:
Download do script da aula
Documentação oficial do Sklearn:
https://scikit-learn.org/stable/

Reconhecimento facial – Treinamento e avaliação do modelo
Se gostarem do conteúdo dêem um joinha 👍 na página do Código Fluente no
Facebook
Link do código fluente no Pinterest
Meus links de afiliados:
Hostinger
Digital Ocean
One.com
Essa aula é baseada no trabalho apresentado no:
Labeled Faces in the Wild: A Database for Studying Face Recognition in Unconstrained Environments Gary B. Huang,Manu Ramesh, Tamara Berg, and Erik Learned-Miller
Para o download da base LFW é só clicar nesse link abaixo:
https://scikit-learn.org/stable/auto_examples/applications/plot_face_recognition.html
Ou da fonte original
http://vis-www.cs.umass.edu/lfw/
Código completo
Esse código é praticamente o mesmo do scikit, as mudanças foram:
Os comentários mais detalhados e em português
Foi adicionado um docstring
Nos prints foi utilizada a formatação mais atual do python 3, o novo mecanismo de formatação de sequência de caracteres conhecido como Literal String Interpolation ou mais comumente como sequências de caracteres F (devido ao caractere f que precede a string). A ideia por trás das strings f é simplificar a interpolação de strings.
"""
================================
Faces recognition example using eigenfaces and SVMs
================================
An example showing how the scikit-learn can be used to faces recognition with eigenfaces and SVMs
================================
================================
================================
Exemplo de reconhecimento de faces usando autofaces e SVMs
================================
Exemplo mostrando como o scikit-learn pode ser usado para reconhecimento de faces com autofaces e SVMs
"""
from time import time
import logging
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.model_selection import GridSearchCV
from sklearn.datasets import fetch_lfw_people
from sklearn.metrics import classification_report
from sklearn.metrics import confusion_matrix
from sklearn.decomposition import PCA
from sklearn.svm import SVC
print(__doc__)
# O logging exibe o progresso da execução no stdout
# adicionando as informações de data e hora
logging.basicConfig(level=logging.INFO, format='%(asctime)s %(message)s')
# #############################################################################
# Download dos dados, se ainda não estiver em disco e carregue-a como uma matriz numpy
lfw_people = fetch_lfw_people(min_faces_per_person=70, resize=0.4)
# Inspeciona as matrizes de imagens para encontrar os formatos das imagens( para plotagem )
n_samples, h, w = lfw_people.images.shape
# para aprendizado de máquina, usamos 2 dados diretamente( esse modelo ignora
# informações relativas a posição do pixel )
X = lfw_people.data
n_features = X.shape[1]
# A rótulo( label ) a prever é o ID da pessoa
y = lfw_people.target
target_names = lfw_people.target_names
n_classes = target_names.shape[0]
print("Total dataset size:")
print(f"n_samples: {n_samples}")
print(f"n_features: {n_features}")
print(f"n_classes: {n_classes}")
# #############################################################################
# Divide a base em um conjunto de treinamento e um conjunto de teste usando k fold
# 25% da base para o conjunto de teste os 75% restantes para o treino
# random_state é para inicializar o gerador interno de números aleatórios
# Definir random_state com um valor fixo garantirá que a mesma sequência de números
# aleatórios seja gerada cada vez que você executar o código
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.25, random_state=42)
# #############################################################################
# Computa o principal component analysis - PCA (eigenfaces) na base de faces
# ( tratado como dataset não rotulado ): extração não supervisionada / redução de dimensionalidade
n_components = 150
print(f"Extracting the top {n_components} eigenfaces from {X_train.shape[0]} faces")
# t0 guarda o tempo zero, para cálculo do tempo de execução do PCA
# O cálculo é feito no time() - t0 do print da linha 81
t0 = time()
pca = PCA(n_components=n_components, svd_solver='randomized',
whiten=True).fit(X_train)
print("done in {0:.3f}s".format(time() - t0))
eigenfaces = pca.components_.reshape((n_components, h, w))
print("Projecting the input data on the eigenfaces orthonormal basis")
t0 = time()
X_train_pca = pca.transform(X_train)
X_test_pca = pca.transform(X_test)
print("done in {0:.3f}s".format(time() - t0))
# #############################################################################
# Treinando um modelo de classificação SVM
print("Fitting the classifier to the training set")
t0 = time()
param_grid = {'C': [1e3, 5e3, 1e4, 5e4, 1e5],
'gamma': [0.0001, 0.0005, 0.001, 0.005, 0.01, 0.1], }
clf = GridSearchCV(SVC(kernel='rbf', class_weight='balanced'), param_grid)
clf = clf.fit(X_train_pca, y_train)
print("done in {0:.3f}s".format(time() - t0))
print("Best estimator found by grid search:")
print(clf.best_estimator_)
# #############################################################################
# Avaliação quantitativa da qualidade do modelo sobre o conjunto de testes
print("Predicting people's names on the test set")
t0 = time()
y_pred = clf.predict(X_test_pca)
print("done in {0:.3f}s".format(time() - t0))
print(classification_report(y_test, y_pred, target_names=target_names))
print(confusion_matrix(y_test, y_pred, labels=range(n_classes)))
# #############################################################################
# Avaliação qualitativa das previsões usando matplotlib
def plot_gallery(images, titles, h, w, n_row=3, n_col=4):
"""Helper function to plot a gallery of portraits"""
plt.figure(figsize=(1.8 * n_col, 2.4 * n_row))
plt.subplots_adjust(bottom=0, left=.01, right=.99, top=.90, hspace=.35)
for i in range(n_row * n_col):
plt.subplot(n_row, n_col, i + 1)
plt.imshow(images[i].reshape((h, w)), cmap=plt.cm.gray)
plt.title(titles[i], size=12)
plt.xticks(())
plt.yticks(())
# Plota o resultado da previsão em uma parte do conjunto de testes
def title(y_pred, y_test, target_names, i):
pred_name = target_names[y_pred[i]].rsplit(' ', 1)[-1]
true_name = target_names[y_test[i]].rsplit(' ', 1)[-1]
return f'predicted: {pred_name}\ntrue: {true_name}'
prediction_titles = [title(y_pred, y_test, target_names, i)
for i in range(y_pred.shape[0])]
plot_gallery(X_test, prediction_titles, h, w)
# plota a galeria das autofaces mais significativas
eigenface_titles = [f"eigenface {i}" for i in range(eigenfaces.shape[0])]
plot_gallery(eigenfaces, eigenface_titles, h, w)
plt.show()
Continuando de onde paramos na aula 15
Treinando um modelo de classificação SVM
Um modelo simples produzido pelo algoritmo Naive Bayes pode se sair melhor do que um SVM executado sem o ajuste de parâmetros.
O “naive” (ingênuo) no nome, é porque ele desconsidera completamente a correlação entre as variáveis (features).
Isto é, se determinada fruta é rotulada como uma maçã se ela for vermelha, redonda e tiver mais ou menos 10cm de diâmetro, o algoritmo vai desconsiderar a correlação entre esses fatores e vai lidar com cada um de forma independente.
Não há desculpa para não fazer o ajuste de parâmetros, especialmente no Scikit Learn, porque o GridSearchCV cuida de todo o trabalho mais chato, mais árduo, é só preciso paciência para fazer a mágica acontecer.
Você não precisa usar o GridSearchCV, você pode escrever todo o código necessário manualmente, mas, talvez não valha a pena.
Sem o GridSearchCV, você precisaria fazer um loop sobre os parâmetros e executar todas as combinações de parâmetros.
Se você estava buscando um resultado com validação cruzada, também será necessário adicionar o código para encontrar os melhores resultados médios de CrossValidation em todas as combinações de parâmetros.
Então, melhor usar o GridSearchCV.
Parâmetros de uma SVM do kernel Radial Basis Function (RBF)
Existem dois parâmetros para um SVM do kernel RBF:
- C
- gama
C
C é um parâmetro do Support Vector Classification(SVC) que irá aprender com os dados, refere-se a penalidade por classificar incorretamente pontos de dados.
Quando C é pequeno, o classificador obtém boa pontuação, mesmo com pontos de dados classificados incorretamente (alta tendência, baixa variação).
C = 1
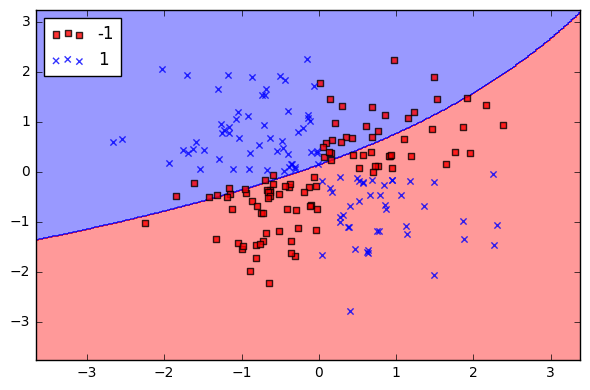
C 1
Quando C é grande, o classificador é fortemente penalizado por dados classificados incorretamente (baixa tendência, alta variação).
C = 10
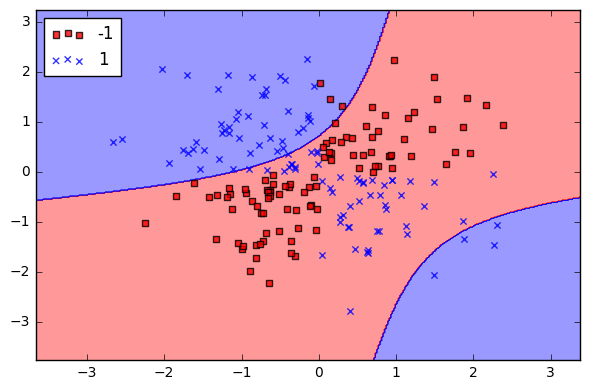
C 10
C = 10000
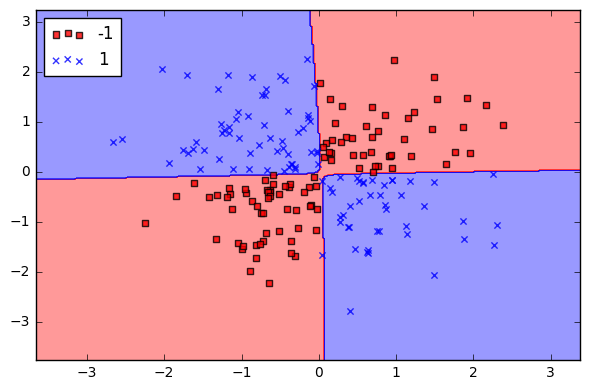
C 10000
Gamma
Gamma é um parâmetro do kernel RBF e pode ser considerado como uma extensão do kernel e, portanto, a região de decisão.
Quando o gamma é baixo(0.01), a “curva” do limite de decisão é muito baixa e, portanto, a região de decisão é muito ampla.
Gamma = 0.01
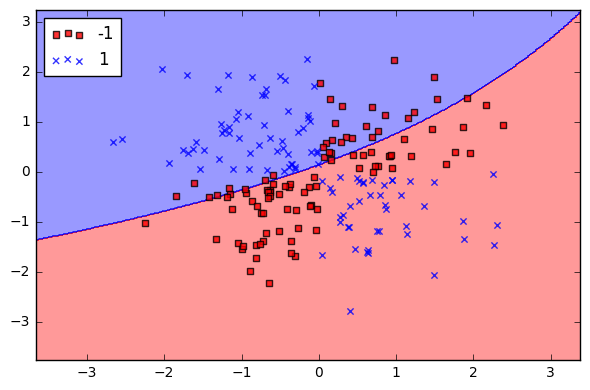
Gamma baixo (0.01)
Quando a gamma é alto, a “curva” do limite de decisão é alta, o que cria ilhas de limites de decisão em torno dos pontos de dados.
Gamma = 1.0
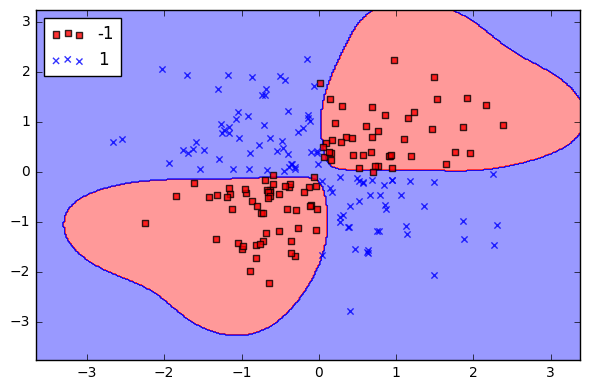
Gamma alto (1.0)
Gamma mais alto ainda.
Gamma = 10.0
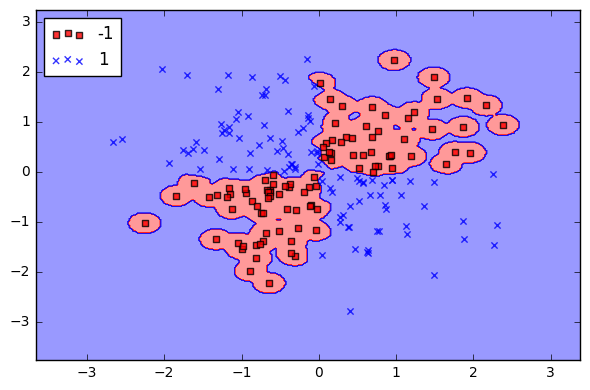
Gamma mais alto ainda (10.0)
Para configurar uma grade de parâmetros(parameter grid) podemos usar múltiplos de 10.
É uma boa opção para começar.
Depois disso, podemos passar o kernel, o parameter grid e o número de validações cruzadas para o método GridSearchCV().
Um exemplo de valores para C e gama é:
param_grid = {'C': [0.001, 0.01, 0.1, 1, 10], gamma: [0.001, 0.01, 0.1, 1], }No exemplo do Scikit, foi usado outros números para esses parâmetros.
param_grid = {'C': [1e3, 5e3, 1e4, 5e4, 1e5], 'gamma': [0.0001, 0.0005, 0.001, 0.005, 0.01, 0.1], }SVC
Usamos no GridSearchCV(SVC(kernel=’rbf’, class_weight=’balanced’), param_grid) o Support Vector Classification (SVC).
O SVC, o NuSVC…, são apenas implementações diferentes do mesmo algoritmo.
O módulo SVM (SVC, NuSVC, etc) é um invólucro em torno da biblioteca libsvm e suporta diferentes kernels, enquanto o LinearSVC é baseado na liblinear e suporta apenas um kernel, o linear.
Então: SVC(kernel = ‘linear’) é o mesmo que LinearSVC()
Em Regressão vetorial de suporte, ou Support Vector Regression(SVR), os parâmetros livres no modelo são C e epsilon.
A implementação é baseada na biblioteca libsvm.
A complexidade do tempo de ajuste é mais do que quadrática, o que dificulta o dimensionamento para conjuntos de dados com mais de duas mil e cem amostras.
Para conjuntos de dados grandes, considere o uso de sklearn.svm.LinearSVR ou sklearn.linear_model.SGDRegressor.
Método fit()
O ajuste, isto é, o método fit() da classe PCA, aprende sobre os dados, principalmente os “componentes” e “variação explicada” (explained variance): clf = clf.fit(X_train_pca, y_train)
Temos a linha do print: print(clf.best_estimator_)
O best_estimator_ pesquisa e escolhe o melhor estimador, ou seja, o que deu a pontuação mais alta, ou a menor perda (se especificado), nos dados de teste, isto é, os dados que ficaram de fora do treinamento.
Não disponível se refit = False.
clf = GridSearchCV(SVC(kernel=’rbf’, class_weight=’balanced’), param_grid, refit=False)
Se refit = False, o atributo cv_results_ não incluirá pontuações de treinamento.
As pontuações de treinamento na computação são usadas para obter informações sobre como diferentes configurações de parâmetros afetam o trade-off de overfitting / underfitting.
No entanto, o cálculo das pontuações no conjunto de treinamento pode ser computacionalmente caro e não é estritamente necessário para selecionar os parâmetros que produzem o melhor desempenho de generalização.
Na próxima aula a gente segue explorando o código, a parte de avaliação quantitativa da qualidade do modelo sobre o conjunto de testes, mas, antes de finalizar essa aula, vamos dá uma revisão, uma recapitulada do que é e como funciona SVM.
Já falamos sobre SVMs na aula 08.
SVM – Support Vector Machine
Para construir o classificador de reconhecimento facial usando o LFW, está sendo utilizado SVM, como já sabemos.
Vamos dá uma recapitulada!
Recapitulando SVMs
Máquinas de vetores de suporte funcionam localizando pontos de dados de diferentes classes e traçando limites entre elas.
Os pontos de dados são chamados vetores de suporte.
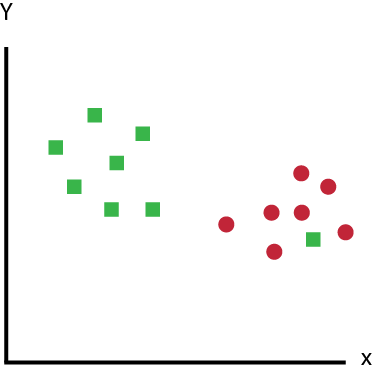
Pontos de dados
E os limites são chamados hiperplanos.
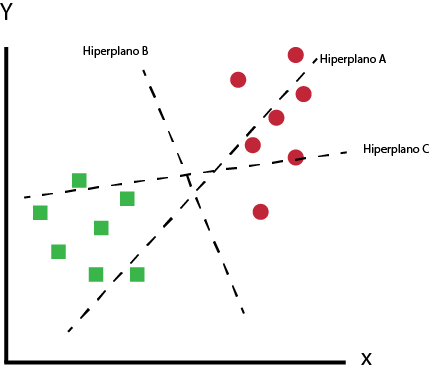
Hiperplanos
Então, o que ele faz é testar várias funções e tentar encontrar a função que melhor separe os dados em suas classes.
Se for uma distribuição linear e bem separada de dados, até mesmo uma reta f(x) = ax + b (função linear) pode separar os dados.
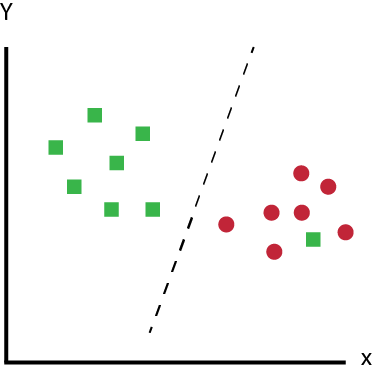
Distribuição linear e bem separada de dados
Mas na maioria das vezes as regiões de classificação se sobrepõem e nenhum único plano reto pode atuar como um limite.
Uma maneira de contornar isso é projetar seus dados em dimensões mais altas, criando dimensões adicionais.
É o contrário do PCA, onde reduzimos a dimensionalidade.
Em vez do espaço bidimensional por exemplo, com as features a e b, você pode combiná-las, por exemplo ab, a ^ 2, b ^ 2 e tentar encontrar padrões, ou um hiperplano dividindo essas dimensões.
Mas há um problema com essa abordagem.
Embora as dimensões extras facilitem a localização de um hiperplano, também oferece ao seu algoritmo mais features para aprender.
Os SVMs nos permitem contornar esse aprendizado adicional usando o truque do kernel.
O truque do kernel
O truque do kernel é uma dessas coisas que está em todas as discussões sobre SVMs, mas, geralmente não é explicada tão bem quanto poderia ser.
Um kernel é apenas uma função que recebe dois pontos de dados como entradas e retorna uma pontuação de similaridade.
Essa semelhança pode ser interpretada como uma métrica de proximidade.
Quanto mais próximos os pontos de dados, maior a semelhança.
O legal das funções do kernel é que elas podem nos fornecer pontuações de similaridade de dimensões mais altas sem precisarmos transformar nossos dados.
Nós conseguimos encontrar os pontos de dados mais próximos em dimensões muito mais altas sem que eles realmente estejam lá.
Isso significa que podemos obter toda a vantagem das features adicionais sem projetá-las e aprendê-las.
O truque do kernel é usar uma função do kernel em vez de fazer uma transformação de alto custo.
Kernels SVM
Você pode escolher entre vários kernels diferentes ao criar seu objeto SVC.
- Linear
- RBF
- Polinomial
- Sigmoid
Para entender cada kernel desses, vamos ver na prática um exemplo, usando o iris dataset.
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm, datasets
def make_meshgrid(x, y, h=.02):
"""Create a mesh of points to plot in
Parameters
----------
x: data to base x-axis meshgrid on
y: data to base y-axis meshgrid on
h: stepsize for meshgrid, optional
Returns
-------
xx, yy : ndarray
"""
x_min, x_max = x.min() - 1, x.max() + 1
y_min, y_max = y.min() - 1, y.max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
return xx, yy
def plot_contours(ax, clf, xx, yy, **params):
"""Plot the decision boundaries for a classifier.
Parameters
----------
ax: matplotlib axes object
clf: a classifier
xx: meshgrid ndarray
yy: meshgrid ndarray
params: dictionary of params to pass to contourf, optional
"""
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
out = ax.contourf(xx, yy, Z, **params)
return out
# import some data to play with
iris = datasets.load_iris()
# Take the first two features. We could avoid this by using a two-dim dataset
X = iris.data[:, :2]
y = iris.target
# we create an instance of SVM and fit out data. We do not scale our
# data since we want to plot the support vectors
C = 1.0 # SVM regularization parameter
models = (svm.SVC(kernel='linear', C=C),
svm.LinearSVC(C=C, max_iter=10000),
svm.SVC(kernel='rbf', gamma=0.7, C=C),
svm.SVC(kernel='poly', degree=3, gamma='auto', C=C))
models = (clf.fit(X, y) for clf in models)
# title for the plots
titles = ('SVC with linear kernel',
'LinearSVC (linear kernel)',
'SVC with RBF kernel',
'SVC with polynomial (degree 3) kernel')
# Set-up 2x2 grid for plotting.
fig, sub = plt.subplots(2, 2)
plt.subplots_adjust(wspace=0.4, hspace=0.4)
X0, X1 = X[:, 0], X[:, 1]
xx, yy = make_meshgrid(X0, X1)
for clf, title, ax in zip(models, titles, sub.flatten()):
plot_contours(ax, clf, xx, yy,
cmap=plt.cm.coolwarm, alpha=0.8)
ax.scatter(X0, X1, c=y, cmap=plt.cm.coolwarm, s=20, edgecolors='k')
ax.set_xlim(xx.min(), xx.max())
ax.set_ylim(yy.min(), yy.max())
ax.set_xlabel('Sepal length')
ax.set_ylabel('Sepal width')
ax.set_xticks(())
ax.set_yticks(())
ax.set_title(title)
plt.show()
Saída:
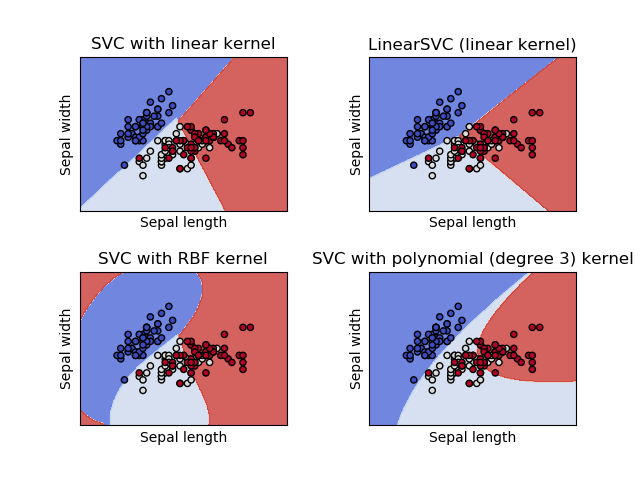
Kernels SVM


O link para a aula 17 está trocado.
Obrigado Flávio, corrigido. Abs.