Aula 01 – complexidade de algoritmos
COMPLEXIDADE DE ALGORITMOS

Complexidade de algoritmos
Voltar para página principal do blog
Todas as aulas desse curso
Aula 02
Se gostarem do conteúdo dêem um joinha 👍 na página do Código Fluente no
Facebook
Esse é o link do código fluente no Pinterest
Meus links de afiliados:
Hostinger
Digital Ocean
One.com
Meu github:
https://github.com/toticavalcanti
Vivemos uma época em que os dados são gerados em enxurradas, hoje em dia quase todo dispositivo gera dados:
- Celulares
- Geladeiras
- GPS
- Sensores
- Cameras
- Luminárias urbanas
- Medidores de poluição
- etc
Cada vez mais, empresas buscam encontrar indicativos, indícios de coisas, preferencia dos clientes, entre outras coisas, em seus dados.
É preciso usar algoritmos muito otimizados para um processamento tão massivo como é exigido hoje em dia.
Então, é muito importante para um programador, saber um pouco sobre complexidade de algoritmos e como é medido o desempenho de um código.
Notação assintótica
- O-grande, ou Big O, é a notação assintótica mais utilizada para determinar a eficiência de um algoritmo
- O Big O descreve o comportamento geral (também chamado de assintótico, pois é o comportamento no limite conforme os dados crescem) do algoritmo em termos do crescimento do número de operações conforme cresce o número de elementos processados (a quantidade de itens é descrita, genericamente, por n)
- É usada para limites assintóticos superiores
O GRÁFICO A SEGUIR ILUSTRA AS CURVAS DE CRESCIMENTO MAIS COMUNS
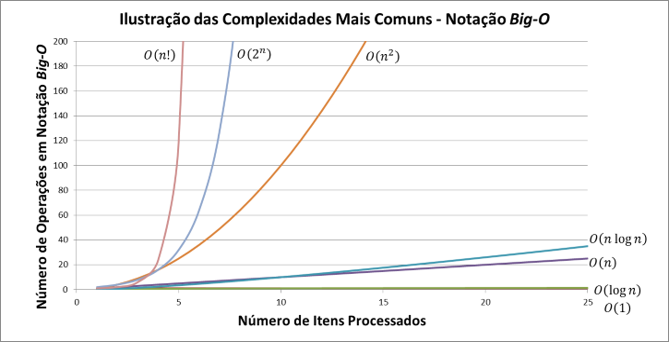
CURVAS DE CRESCIMENTO MAIS COMUNS
DESEMPENHO
- O (n!)(fatorial) o número de instruções executadas cresce muito rapidamente para um pequeno crescimento do número de itens processados. É o caso da implementação ingênuo do problema do caixeiro viajante ou de um algoritmo que gere todas as possíveis permutações de uma lista.
- O (2^n)(exponencial) também é bem ruim, pois o número de instruções também cresce muito rapidamente (exponencialmente), ainda que numa taxa menor do que o anterior. É o caso de algoritmos que fazem busca em árvores binárias não ordenadas
- O (n^2) (quadrático) é factível, mas tende a se tornar muito ruim quando a quantidade de dados é suficientemente grande. É o caso de algorítmos que têm dois laços (for) encadeados, como, por exemplo, o processamento de itens em uma matriz bidimensional.
- O (n log n) (sub-quadrático ou super-linear) é melhor do que o quadrático. É o caso do algoritmo de ordenação QuickSort, tem complexidade C(n) = O(n²) no pior caso e C(n) = O(n log n) no melhor e médio caso.
- O (n) (linear) é aquele cujo crescimento no número de operações é diretamente proporcional ao crescimento do número de itens. É o caso de algoritmos de busca em uma matriz unidimensional não ordenada.
- O (log n) (logaritmo) é aquele cujo crescimento do número de operações é menor do que o do número de itens. É o caso de algoritmos de busca em árvores binárias ordenadas (Binary Search Trees).
- O (1) (constante) é aquele em que não há crescimento do número de operações, pois ele independente do volume de dados de entrada (n). É o caso do acesso direto a um elemento de uma matriz.
COMPLEXIDADE DE ALGORITMOS O(1):
arr = [4, 5, 3, 9, 7]
arr[4]
7
Outro exemplo:
arr = {"odd":1, "even":2}
arr["odd"]
1
COMPLEXIDADE DE ALGORITMOS O(log n):
Na busca binária é necessário ordenação. Então considere a lista ordenada a seguir.
lst = [1, 3, 45, 59, 60, 83, 90]
Suponha que o elemento desejado é o número 83.
A busca tenta encontrar no meio da lista ordenada o 83, mas encontra o 59.
lst = [1, 3, 45, 59, 60, 83, 90]
A busca verifica se o 83 é maior ou menor do que o 59 e constata que é maior.
A busca verifica se o 83 é maior ou menor do que o 59 e constata que é maior.
O espaço de busca agora foi reduzido pela metade
lst = [1, 3, 45, 59, 60, 83, 90]
A busca agora se restringe a lista da posição 4 à 6, ou seja, do 60 ao 90.
A busca tenta encontrar no meio da lista ordenada o 83, e dessa vez encontra o 83.
lst = [1, 3, 45, 59, 60, 83, 90]
COMPLEXIDADE DE ALGORITMOS O(n):
arr = [4, 5, 3, 9, 7]
for item in arr:
print(item)
Outro exemplo:
def summ(n):
if n <=0:
return 0
return n + summ(n - 1)
COMPLEXIDADE DE ALGORITMOS O(n^2)
arr = [1,3,5,7]
for i in arr:
for j in arr:
print(i+j)
COMPLEXIDADE DE ALGORITMOS O(√n)
def func_a(n):
s = i = 1
while s <= n:
i += 1
s += i
print(" Olá ")
s – 1, 3, 6, 10, 15, 21, … n
i – 1, 2, 3, 4, 5, 6, …
O loop vai parar depois k iterações.
Ou seja, depois de k iterações o valor de s será maior ou igual a n.
O loop vai parar depois k iterações.
Qual o valor de s depois de k iterações?
Ou seja, depois de k iterações o valor de s será maior ou igual a n
O loop vai parar depois que:
k(k + 1) / 2 > n
k^2 + k / 2 > n
k = O(√n)
Outro exemplo de complexidade O(√n)
a(){
i = 1
for(i = 1; i^2 <= n; i++)
printf("Toti")
}
for(i = 1; i <= √n; i++)
COMPLEXIDADE DE ALGORITMOS O(n!)
def factorial(n):
if (n == 1):
return 1
else:
return n * factorial(n-1)
É isso, nos vemos na próxima. 🙂
Aula 02
Todas as aulas desse curso
Voltar para página principal do blog
Se gostarem do conteúdo dêem um joinha 👍 na página do Código Fluente no
Facebook
Esse é o link do código fluente no Pinterest
Meus links de afiliados:
Hostinger
Digital Ocean
One.com
Meu github:
https://github.com/toticavalcanti
Obrigado, até a próxima e bons estudos. 😉